• Hexmozaix Jr.
• Multimatch I
• Multimatch II
• Multimatch III
• Multimatch IV
• Marshall Squares

• Triangoes
• Triangoes Jr.
• Cookie Jar
• Hexmozaix
• Hexmozaix II
• Arc Angles
• LineDance
• Rhominoes

• Kaliko
• Dezign-8
• Diamond Rainbow
• Boats
• Puzzabilities
• Rhom-Antics

• Tri-Chex
• Snowflake Super Square
• Snowflake Square
• Trifolia
• IZZI 2
• Color Cube Sudoku
• Color Up

Here is the puzzle set that inspires love at first sight for young and old. The 24 little hexagon tiles (see sample below) are hand-inlaid with diamonds in all combinations of four colors. Match them by color to solve patterns, create designs, and play several games. The basic figure fits into a 7½" rounded triangular acrylic tray. The center holds a blank tile that serves as a free space. For 1 to 4 players, ages 6 to adult. $59

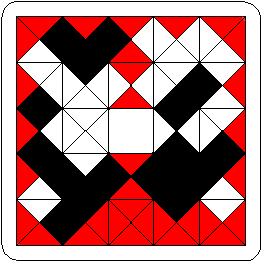This is the set that started it all—the classic 3-color set of 24 all-different edge-colored tiles ("MacMahon's Three-Color Squares"), first proposed in 1921. See sample tile at right. Match them by color to create interesting symmetrical shapes. The harder challenge is to do it so the border is the same color all the way around. The 4x6 rectangle with uniform border has 13,328 solutions! The book encompasses thirty years of research into this set by Wade Philpott. And we've added an aspect MacMahon never mentioned—how to form intriguing color patterns in the interior of a solution. Rules for several games are also included. The hand-inlaid 1½" acrylic tiles fill their 8½" tray with one space to spare. Color mix may vary. For 1 and 2 players, ages 8 to adult. $65

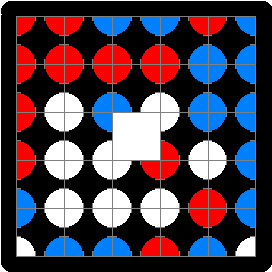
We've turned the divisions on the Multimatch I tiles from diagonal to vertical/horizontal to get this other set of 24 unique 3-color squares. Here the color-matching gets trickier because each edge has two segments to be matched up. Even so, the 5x5 with the central hole has 17281 solutions, as derived by researcher Toby Gottfried's computer programs. A great many puzzle designs are presented, including some non-match themes, and several games, including the sliding game "Slot Machine." Hand-inlaid, brightly colored 1½" acrylic tiles in 4 color schemes, plus one clear window, fill the 8½" tray. For 1 to 4 players, ages 8 to adult. $65

This is the second of MacMahon's classic sets of color tiles first proposed in 1921. The 24 edge-colored triangles have all-different patterns with 4 colors. These, too, allow a series of color-matched designs with just one color around the outside edges, as discovered by Wade Philpott. Several games and new color patch designs are our more recent contribution. All acrylic, hand-constructed tiles form a hexagon in their 8½" tray. Your choice of bold, blue-lagoon or warm colors. For 1 or 2 players, ages 8 to adult. $65

This handsome relative of Multimatch III is twice as tricky, because two segments of color show on every edge. The illustrated manual contains many puzzle designs for color mixing and matching, and some competitive games. The 24 handfitted acrylic tiles, in bold, cool-pool or warm colors, represent all the combinations with four colors. Oddly enough, they cannot fill the hexagon in its 8½" tray with complete colormatching, but their opposite-color symmetries are all the more beautiful. For 1 or 2 players, ages 8 to adult. $65

This intriguing set of 25 unique tiles became one of the "25"-themed tributes to our 25th anniversary. William invented it in 1983 in high school. We thank Jacques Haubrich for introducing it to us. The squares are edge-colored (like Multimatch I) and have one or two colors shared equally, in every combination of 5 colors (see samples at right). As a 5x5 square it has 16 basic solutions. Jacques' computer found that 3 of them have a solid-color center but no solid corners. Overall, the 5x5 has 3840 physically different solutions. The diagonal design at left is by Kate Jones; the elegant solution with solid tiles at the outer corners is by Jacques, who also found that this figure has no solution with a solid tile in the center! Toby Gottfried also found an amazing symmmetrical solution. All acrylic, 8½" tray. Colors may vary. Includes Kate's original strategy game "Trade" that rewards interactions between players. For 1 to 5 players, ages 8 to adult. $65