See also the 25 Holes Challenge.
You may win a silver dollar!
(Link opens in new window.)

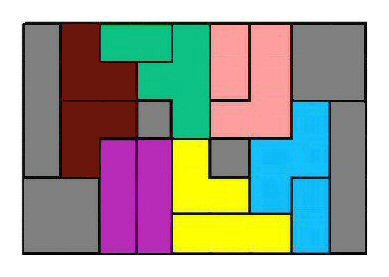
This sweet and innocent-looking set of 21 V-shaped trominoes (3 squares each) can entertain a four-year-old with simple patterns, yet infuriate a grown-up expert with tough challenges. See, for example, the three-color problem. Math professor Norton Starr originally commissioned this set to demonstrate proof of a theorem, that an 8x8 grid can be filled with trominoes no matter where you leave the empty space. We coupled this with a color-separation feature, then added an original puzzle concept by Oriel Maximé, of filling the Vs on grids around strategically placed barricades. The 28 "Bends" layouts cover four levels, from Easy to Expert. Other challenges and game rules are included. A feature discovered later and added in the second edition of the book is a pretty alphabet. All acrylic, 7 tiles each of 3 luminous transparent colors in 7" tray with engraved grid lines. You can choose from three color combinations. Ages 4 to adult, 1 or 2 players. $42

Add to your order

One of our constant bestsellers! All the shapes of 1 through 5 squares in size (polyominoes orders 1 through 5) fill a 6" tray. The colorful lasercut acrylic pieces also serve for six games and hundreds of other puzzle shapes, as shown in the 52-page handbook. Here is an elegant alphabet by Ken Blackledge. See also rare solutions and the special Anniversary designs we created with the full Poly-5 set for the 25th annual Maryland Renaissance Festival (2001), 50th annual Three Rivers Arts Festival, 40th annual Syracuse Arts & Crafts Festival, 40th annual Greensboro Craftsmen's Christmas Classic, 30th annual Verona Fine Art and Crafts, 30th CHAP convention, 50th annual Artsfest of Greater Harrisburg, and Kadon's own 30th Anniversary and 35th Anniversary. For 1 to 4 players, ages 8 to adult. Poly-5 is available in five color choices. $42

Our bestselling Poly-5 in beautifully hand-stained and polished wood, lasercut for precise fit. The game board is engraved into the back of the tray, with a jazzy border design. Same shapes of pieces and same 52-page book of 6 games and hundreds of puzzle challenges as for the standard Poly-5 (above). For 1 to 4 players, ages 8 to adult. $65

Jason Ancheta developed this modular kit of geometric tiles originally for his daughter, Jaslyn Joy, as a foundation for spatial visualization and reasoning. So we named it after his daughter and expanded it for educational fun for students, homeschooling and classrooms, also providing endlessly fascinating discoveries for grown-ups in recreational mathematics. As you can see, this whole section features our many polyomino sets. This detailed new primer helps to summarize their major concepts.

Polyominoes, so named by Solomon Golomb in 1953, are based on joining squares to form countless shapes. The tiles in this set contain 1, 2, 3, and 4 squares. The 6 color pairs hold 6 squares each, as 4+2 and 3+3. The 6 neutral pieces complete all the shapes in these sizes. For storage and artistic display, find ever new solutions for the 6x9 tray. Challenges include framing, building, alphabets, doubling, tripling, and matching polyominoes sizes 4 through 6 — each size with its own special name: tetrominoes, pentominoes, hexominoes. Engraved vinyl 15x15 grid game mat included. For 1 to 2 players, ages 6 to adult. $65

36 acrylic pieces include all the shapes of 6 squares joined ("hexominoes"). Each piece has a name. They are sized to be compatible with Poly-5, for those who want the extra excitement of combining the whole series. The 8˝" tray and game grid accommodate four strategic games and hundreds of puzzles. Sextillions is available in several color combinations. For its 25th anniversary in 2009, we gave it a frosted silver frame and center, and a special "25" solving challenge (.pdf, opens in new window). Suitable for 1 to 6 players, ages 12 to adult. $65

This set of the 108 shapes of 7 squares joined ("heptominoes") is for only the most dedicated. Three colors form congruent rectangles, each with a center hole, in a 13x18" acrylic tray with lid. This is the famous solution originally found by David Klarner decades ago. Here are some different solutions by dedicated solvers. See also this amazing collection of intricate heptomino figures by Nick Maeder. The pieces are sized to fit with Poly-5 and Sextillions for those who want to try mega-combinations. No instructions; you're on your own with this one. Heptominoes set is available by special order only. Please indicate 3 color preferences. $225

NOW!   See Chunky-Octs, a 20-piece subset of Octominoes, masterminded by Rodolfo Kurchan for super fun!

Okay, so we don't know when to leave well enough alone. This expanse of 369 different shapes holds all the ways eight squares can be joined. The elegant solution shown, as three congruent rectangles, is by David Bird. Notice how he saved the simpler, chunkier shapes to the last, where you see them clustered together in the lower rectangle.

Six pieces, symmetrically centered, have an unfillable enclosed space, so we dot those with contrasting colors. We thank Professor Jack Wetterer for inspiring us to switch to this pattern. Here is a different solution, which served for the original version in custom-built wooden showcase with clear cover. Then feast your eyes on this 20x148 octominoes rectangle by Lewis Patterson, with neatly placed holes at each end, and his incredible 79x147 enneominoes (order-9) rectangle. And here is a mega-solution by Karl Wilk that incorporates the octominoes in a solution of polyominoes 1 through 9.

Our Octominoes are served up without instructions, in a 23x47" tray with lid, suitable for hanging on a sturdy wall or even turning into a coffee table. The lid fastens with 6 decorative brass acorn bolts (not shown).

Available by custom order only. Please indicate a color preference from our transparent colors, and give us at least one month to make it.

Need we say this set is suitable mainly for teen and adult puzzle champs? $550
(plus $25 oversize shipping surcharge)