In October 2012, Doug Caine sent us this slightly modified version that even has all colors grouped:

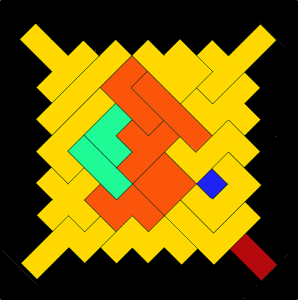
If we count the one non-pentomino as occupying 5 unit edges of the perimeter, is there a way to get it down to 4? Can you do better or prove the solutions shown above are, indeed, the best result possible? A prize for such an answer! Email your solutions to Poly-5 Perimeter.

Another rare solution is to have the smallest pieces form a square in the center. Here is one example, though one orange corner is touching it.

Here's the square off-center, floating in a sea of the pentominoes, and the colors symmetrically grouped, solved by Eric Bare:

The further question is, can the small square be centered and surrounded entirely by only a single color? Yes, and George Sicherman found it and won a prize for this beautiful solution. Again, the colors are grouped.

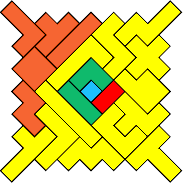
Two other tricky challenges were the tetromino center line (left, in blue) solved by Meshele Merchant, and the smaller pieces separated around the perimeter (right), by Eric Bare. It's interesting that these solutions were found for the first time after more than 25 years of our making this puzzle. There is no end...

In June 2016, Kate found this rare solution that has only four unit edges that are not pentominoes:

Nathan Gilbert set a new record with his solution that has only 4 unit edges that are not pentominoes, and for good measure he also grouped the interior pieces, which don't touch the border even at a corner. Wow, Nathan!

In 2019, Kate found this solution with the center line formed by the straight pieces from 1 to 5, with the unit square in the center and no part of the center line touched by any piece of their own color. It was harder to solve than it looks:

In April 2022, Teri Saunier posted this splendid solution on the Kadon Gamepuzzles^® Universe Facebook page, with the trominoes and tetrominoes forming a double center line.