|
Trapezoid Competition 2009
is now closed. See winning results below.
Jacques Ferroul offered prizes for the best solutions to a two-fold TRAPEZOID challenge during 2009. The winner of both challenges was Robin King, of New York, NY. Congratulations, Robin!
The challenges
The winning solutions (links open in new window)
Here are two of the longest trapezoids of each challenge. See the full sequences on Jacques' pages linked above.
- With spare triangles (3
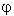 +9): +9):

- With only the polyores (8
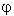 +1): +1):

Details
Lengths of sides of the trapezoids are counted in units of the sides of the golden triangles. The longer dimension (the sides of the tall triangle and base of the wide triangle) is called phi (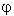 ); the shorter dimension (the sides of the wide triangle and base of the tall triangle) is simply "1". ); the shorter dimension (the sides of the wide triangle and base of the tall triangle) is simply "1".
Jacques enumerated 148 different sizes of trapezoids, where x is the length of the top horizontal side. For the special case where x=0, it's the tip of a triangle. The oblique sides of each trapezoid in the series are always the same length: 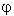 +1. The bottom horizontal sides have the length of x+ +1. The bottom horizontal sides have the length of x+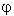 . So the height of the trapezoids stays constant while they progressively stretch sideways like an accordion. . So the height of the trapezoids stays constant while they progressively stretch sideways like an accordion.
We list here the 148 sizes. It is not known whether each has a solution. The competition did not require a solution for all 148, only the longest continuous sequence within the series. If one was skipped, that ended that streak. Here's a sample trapezoid of size 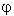 : :
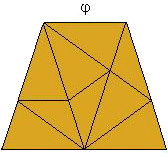
The dimensions for x:
Each solution has a different combination or "inventory" of the two unit triangles. For example, the sample size shown above contains 6 tall and 3 wide triangles. Jacques' website shows the inventory for a few other sizes.
Although this contest is closed now, we encourage you to explore further solutions for your own enjoyment of La Ora Stelo. If you ever beat the results of the winning solutions reported here, send us a drawing anyway, and we will add it to the records. Win fame, not money.
Kadon Enterprises, Inc.
| 

