Page
1 of 5 		Naming the Hexacube Pieces
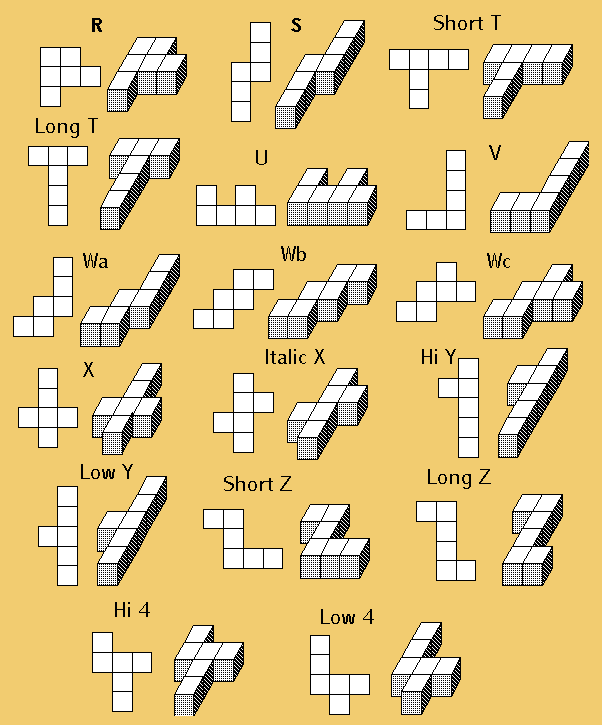
The 166 uniquely shaped hexacube pieces are based on the shapes of six cubes joined on their faces in all the possible different combinations. They are the sixth-level members of a family of shapes known as "polyominoes" and "polycubes," originally defined and named in 1952 by Solomon Golomb, as published in his book, Polyominoes.

The most popular and friendly group of such shapes are the pentominoes (5 unit squares/cubes joined), sold by Kadon under the name Quintillions. Golomb gave the individual pentominoes names that are easy to remember, because they look quite a bit like letters of the alphabet.

We have extrapolated and extended the logic of this naming system to the 166 hexacubes. Our naming system was first published in 1987 when we began constructing Hexacube sets. It is the only naming system that relates the name to the shape for ease of remembering and identification. Other schemes, such as simply numbering the pieces from 1 through 166, are not practical for human use, only for computer modeling. Naming a piece according to its shape structure is the most logical and useful method.

We present them here in four related groups, based on the size of their cross-section, and explain them in greater detail with their illustrations. The 166 shapes occupy 5 pages. You can visit any page by clicking the number buttons on the bottom of each page, or click on "Continue" to go to the next page.

The cross-sections range from 6 to 3 unit cubes in size:

  • The first group has all the flat or planar hexacubes, of which there are 35 distinct shapes with cross-section of 6.

  • The second group has the 72 pentomino derivatives (from the 12 planar pentacubes with cross-section 5), formed by attaching a single cubelet on top or bottom in all the different possible positions. Thus a single pentomino may have anywhere from 2 to 5, 6, 9 or 10 offspring, depending on the symmetry of the original pentomino shape.

  • The third group has 53 tetracubes plus domino, a 1x1x2 piece attached in all the different possible positions on the top or bottom of a 4-unit cross-section, plus a few that have two separate single cubes.

  • The fourth group has 6 shapes based on a V-tromino 3-unit cross-section, and a V tromino attached on top in all its possible different positions.


Group 1 — largest cross-section of 6 unit cubes
Let's get a closer look. Here is how the flat hexacubes look from a bird's-eye view, with lines marking their division into squares, and as 3-D objects showing their division into cubes. They are shown in the position that makes them especially easy to visualize: in alphabetical order, with every letter represented except B, and the number 4 added at the end. Some need to be viewed diagonally. Some letters do double duty for long and short, or high and low models.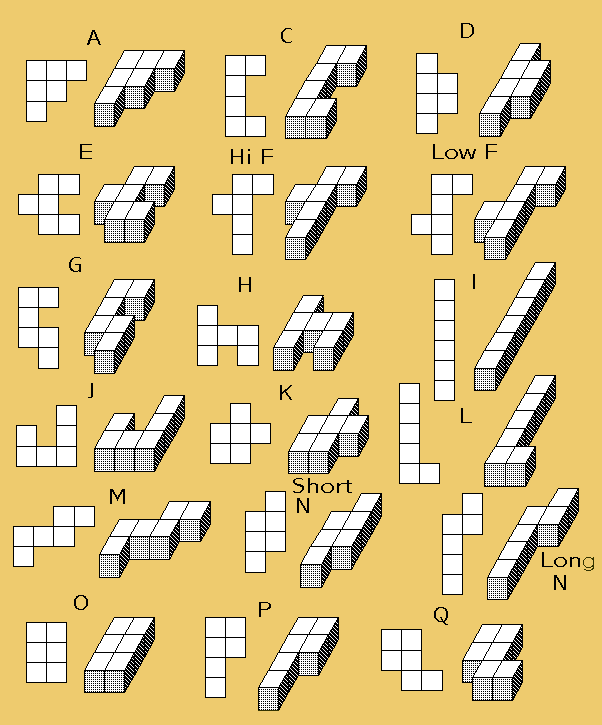

The planar hexacubes




©2001-2012 Kadon Enterprises, Inc.