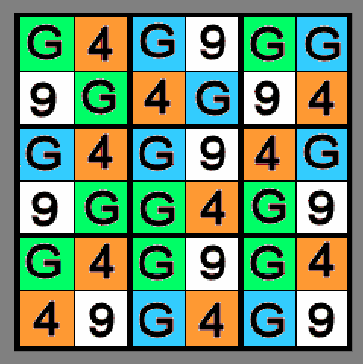The THREE-SQUARED CHALLENGE

presented by Kate Jones
to the attendees at Gathering for Gardner 9
March 24-28, 2010 — Atlanta, Georgia
 

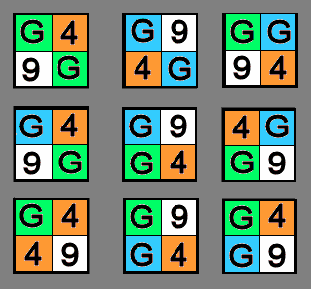
The Three-Squared Challenge is made of 9 corner-colored squares. Six tiles have four colors each, in every possible order. The other three tiles have 3 colors each, with duplicate colors on opposite corners (“bow-ties”). The four colors divide into 8, 9, 9 and 10 units, respectively. And further, each color has been assigned one of the four characters: G – 4 – G – 9. Puzzlers are asked to cut out the pieces around the outlines and assemble them to solve several puzzle tasks.
 

 
Some goals for the 3x3:

1. Arrange the tiles to display 9 groups of G4G9, in that order, in 4 adjacent unit squares in a straight line. Rows can be horizontal, vertical, diagonal, up, down, sideways or backwards. Tiles can be rotated as needed. Colors don’t count.
2. Match all tiles by color (disregard the printed characters).
3. Have no two of the same color touch sides. Vertex contact is OK.
4. Create symmetry with one or more colors (all four are possible) while non-matching.
5. Maximize color pairs (16 dominoes).