Into our second decade, and having introduced many products from very small to very large, this was our year to let loose our most difficult sets into the world. Most of these are absolutely not for children. Here are their start-ups:

But, oh, the Herculean task of getting the pieces to solve figures! Having all pieces in the same color looked boring, so Kate had the brainstorm to use three colors and find a map-colored solution. Years later we learned from computer solvers that the solution she had found that allowed for just three colors to fit without edge-touching indeed has only one solution. And it was yet more years later that we finally printed the voluminous book the set needed and deserved. Rhombiominoes is for only the most determined solvers! The solution here uses just 15 pieces and two colors per mini-rhomb.
 

Quintachex^®
After two false starts of making this wonderful concept in cardboard and die-cut rigid vinyl (see notes for 1985 and 1988), and a short interlude of making it in very labor-intensive wood, we found the ideal medium of laser-cut acrylic. Because the 13 tiles are two-sided, each side inlaid with its own color assignment, precision was needed and the right "feel" of weight and placement. And we could change its colors from set to set since we make one set at a time instead of the commitment of a large print run. An expanded booklet with a repertoire of beautiful if tantalizingly difficult challenges soon followed. For its Silver Anniversary year we added silver as one of the colors. Should you want to use it as a checkerboard when successfully solved, inquire about getting matching little checkers.
 

Multimatch^® IV

We had already explored and produced several colormatching ideas, including the edge-colored and corner-colored squares and edge-colored triangles introduced in 1989 as Multimatch I, Multimatch II, and Multimatch III. The missing member of this series was the 4-color set of corner-colored triangles, which proved to be the most vexing to wrestle into matched solutions, although they surprised us by making awesomely beautiful opposite-color symmetries. This set joined the three earlier members of the Multimatch family as Multimatch IV. It looks fantastic with some of our new frosted-color acrylics.
 

Tan Tricks III^TM
This giant companion to the already difficult Tan Tricks I and II adds 107 unwieldy pieces and amazingly can form a square with six unit triangles supplied as fillers. Each tile consists of 6 isosceles right triangles (squares cut in half diagonally), so there is a strong prevalence of long diagonal streaks in a solution, with the intact little squares mostly buried. There are thousands of solutions, though none of them volunteers to show up when you are trying to fit them all into their tray or build other figures. The one solution we show took 40 human hours to solve. It wouldn't have been fun nor fair to use a computer to solve it, though we wouldn't mind consulting a computer to tell us the total number of solutions!

Trifolia^TM
Following the expansion of our "edge-matching" category and the success of the exquisite Snowflake Super Square which matched edge shapes instead of edge colors, the idea arose to give triangles the same treatment. Inspired by M. C. Escher's tessellations and drawing on its cousin Multimatch III's wealth of material, we added our own further research, graceful style and checkerboard coloring, plus original games. The packing solution incorporates Kate's goal of having the three Trifolia pieces—that have all three edges the same shape—form the corners of an interior triangle. The checkerboarding was superimposed upon that solution.

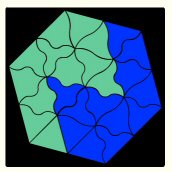A few years later, in 2001, a small controversy arose intercontinentally, with puzzlers pondering why, with 12 tiles of each color, the hexagonal tray could not be filled with a straight division of the two colors, half and half. Much analysis and mathematical gymnastics ensued, and at last Toby Gottfried's computer program found 2,320,810 solutions but not a single one with a perfect split of colors. Jacques Haubrich found, however, that there are 297 ways to make a checkerboarded array. Toby found that only 7 of those solutions have the three triple tiles as in Kate's original apex design. His research also turned up 173 solutions for the two colors to be grouped, of which Jacques identified that only 3 have congruent colors as well. Here's one. Thank you again, gentlemen, for this wondrous synergetic collaboration in advancing human knowledge!

Polyarcs^TM
This clever polyform set invented by math educator Henri Picciotto came our way through our former associate, Michael Keller, publisher of the great, late game review magazine WGR, a rare and precious compendium of game and puzzle lore published for only 13 issues, jampacked with intelligent and thorough research serving a world-wide readership. Michael's website, Solitaire Laboratory, is rescuing that historic material and continuing the good work. As interest in Polyarcs grew from reviews and comments in math circles, we started making them in very small quantities, mostly as folks asked for them. Eventually we gave it its own showcase in our website as an honorary member of our growing family of polyform puzzles. Visit Henri's website for a lot more background information. "Polyarcs" is a trademark of Henri Picciotto, used by Kadon by permission.

Shadow Play^TM
This little set was a reprieve from our line-up of dramatically difficult doings. It brought mind expansion of the creative kind.

We had started hearing from people all over the world who found us online or in reviews. One of these was Parakum Maitipe, a creativity researcher in Sri Lanka. He proposed a set of 9 geometric shapes that he had selected for maximum variety and compatibility. They draw on the players' creative imagination, concentration, and powers of visualization. Shadow Play touches on how the mind makes complex coherent images from the simplest abstract shapes, or order out of chaos. It recalls the fun people have seeing images in clouds, or interpreting Rorschach inkblots or tea leaves.

With Shadow Play, one player constructs an image that another player will try to guess. How real can you make it? This great idea of Parakum's goes beyond tangrams, where players solve existing figures, to opening the mind to endless creation. It's an ideal tool for classrooms, creativity workshops, brain training programs, and sheer fun and relaxing improvisation for individuals, akin to meditation. The power of suggestion is also the key to finding new answers to old quandaries.

While any group of tiles and particles can serve such purposes, Shadow Play has the finest mix we could think of for both aesthetics and versatility. We have collected hundreds of designs and keep looking for more. Send us your best ones.
 

The year 1990 saw us reach new heights in productivity, with more shows stretching from Florida to Michigan, more awards, more pages in our print catalog, and more delightful research into new ideas. Releasing the most difficult puzzles gave us the boost to trust the world to accept the full extent of our work as art. Finding our true voice was our ninth rule.
 

1999-2024:   Finding kindred spirits